算法-计算圆周率pi值，精确到小数点后5位

题目

Given that Pi can be estimated using the function 4 * (1 – 1/3 + 1/5 – 1/7 + …) with more terms giving greater accuracy, write a function that calculates Pi to an accuracy of 5 decimal places.
翻译：给定pi=4 * (1 – 1/3 + 1/5 – 1/7 + …)的计算公式，项越多越精确，写一个方法来计算得到精度为小数点后5位的值

本来是在看博客：20个有争议编程的观点（其实我都很赞同，除了第19条，我还是支持优秀的设计是需要合适设计模式的），突如其来出现了一个面试算法题，思考分析了下发现其实考验的是数学题，以下是我的分析求解过程

分析过程

圆周率从小学就开始背诵了，现在还是记得清清楚楚，π=3.141592657...，所以小数点后5位那就是3.14159。

求和

圆周率π的计算有很多中方式，此题已经给出了π的无穷级数，通过python实现其求和:

def calculatePi(x):
    pi = 0
    for i in range(0, x+1):
        tmp = (2 * i + 1)
        if i % 2 == 0:
            pi += 1 / tmp
        else:
            pi -= 1 / tmp
    return 4 * pi

目标x的值

通过无穷级数累计就和即可得到pi,但pi是一个无理数，不可能有一个精确的值，计算只能无限逼近理想值，这题的关键就是小数位后5位精度，从判断这个精度如何达到的角度切入,推导后直接能算出精度截止到小数点后5位时x的目标值

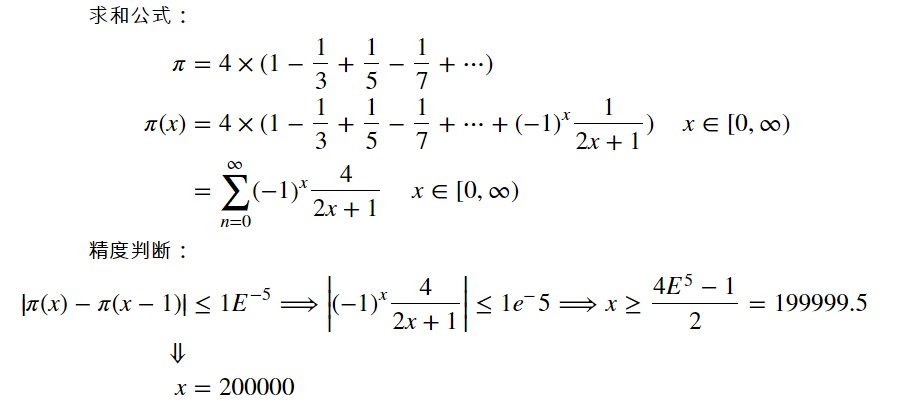
得到x的目标值为200000，代入求和公式即可得到π的结果

$ calculatePi(200000)
3.141597653564762

推导过程学习是在python jupyter notebook中使用了下LaTeX语法，但hexo若要支持laTeX需要额外安装插件和配置。

$$
\begin{align}
\pi & = 4 \times (1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \cdots) \\
\pi(x) &= 4 \times (1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \cdots + (-1)^{x}\frac{1}{2x + 1}) \quad x \in [0,\infty) \\
&= \sum_{n=0}^\infty (-1)^{x}\frac{4}{2x + 1}  \quad x \in [0,\infty)\\
\left | \pi(x) - \pi(x - 1) \right | &\leq 1E^{-5}    \Longrightarrow \left | (-1)^{x}\frac{4}{2x+1}\right | \leq 1e^-5 \Longrightarrow x \geq \frac{4E^5 -1}{2} = 199999.5 \\ 
\Downarrow \\
x &= 200000 
\end{align}
$$