算法实践-堆排序

堆排序

堆排序使用完全二叉树的数据结构，在STL中虽然有heap，但属于一种算法，而不是一种容器。
堆排序的过程是每次将最大数字从最大堆中一个个提取出来，直至成为一个有序数组。
其空间复杂度为O(1)，时间复杂度是O(NlogN)，没有最坏时间复杂度。对比起快排，最坏情况下是O(n^2)，
为何堆排序没有快排应用多呢？
知乎找到一个豁然开朗的答案：

堆排比较的几乎都不是相邻元素，对cache极不友好。数学上的时间复杂度不代表实际运行时的情况

待会的排序过程便可以看到堆算法堆缓存极其不友好了。

堆排序过程

堆排序过程具体分为两个步骤：

1. 建立最大堆
2. 每次从最大堆中弹出最大值

这两个步骤循环结束即可得到排序数组。所以一次介绍这两个步骤的具体实现。

建堆

堆排序的性质是用一个数组存储完全二叉树，从索引i从0开始填有如下3个性质：

1. i节点的左子节点在2 * i + 1
2. i节点的右子节点在2 * i + 2
3. i节点的父节点则在(i - 1)/2

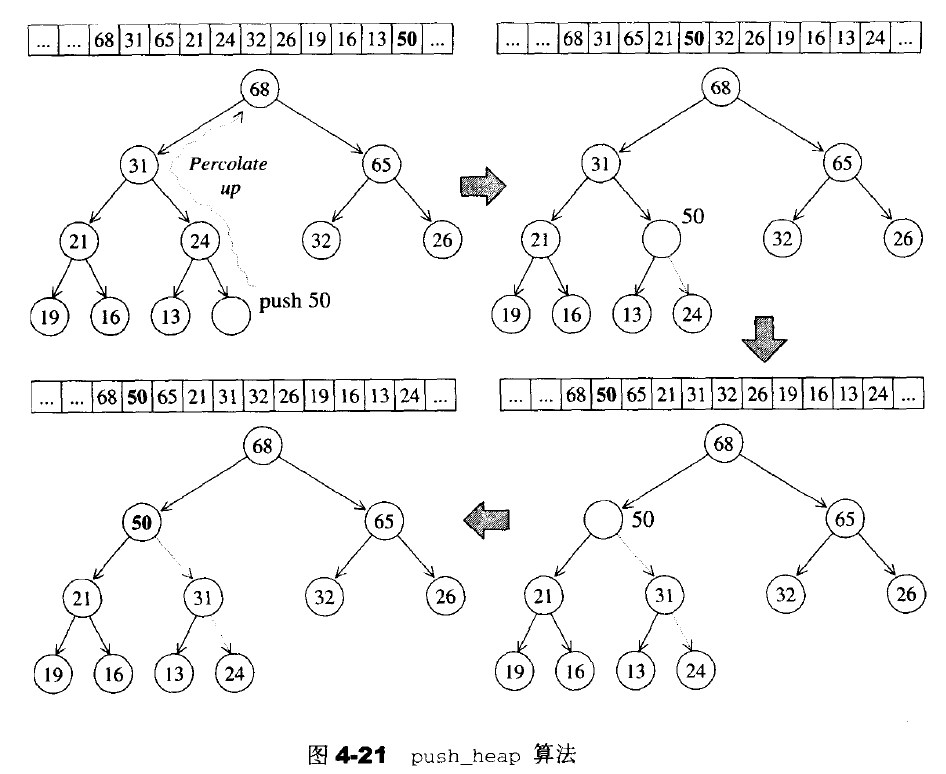
建堆的策略是从数组头开始，每次往堆中添加一个元素，这个元素不停和它的父节点比较，大于父节点就互相交换，交换之后从当前父节点上溯比较其祖父节点，直到遇到小于它的父节点截止。来看一下**STL源码剖析上的解释图更容易理解：

void make_heap(int* arr, int length){
    int parentIndex, childIndex;
    for(int i = 1; i < length; ++i){
        childIndex = i;
        parentIndex = (i - 1) / 2;
        while(parentIndex >= 0 && arr[parentIndex] < arr[childIndex]){
            swap(arr[parentIndex], arr[childIndex]);
            childIndex = parentIndex;
            parentIndex = (childIndex - 1) / 2;
        }
    }
}

如果有最大堆已经有1000(index为999)个元素了，最新添加的第1001(index为1000)个就要去找其父节点index为499的节点元素，如果内存页大小比较小或者这个堆更大的话，很容易就跨页访问元素。

排序

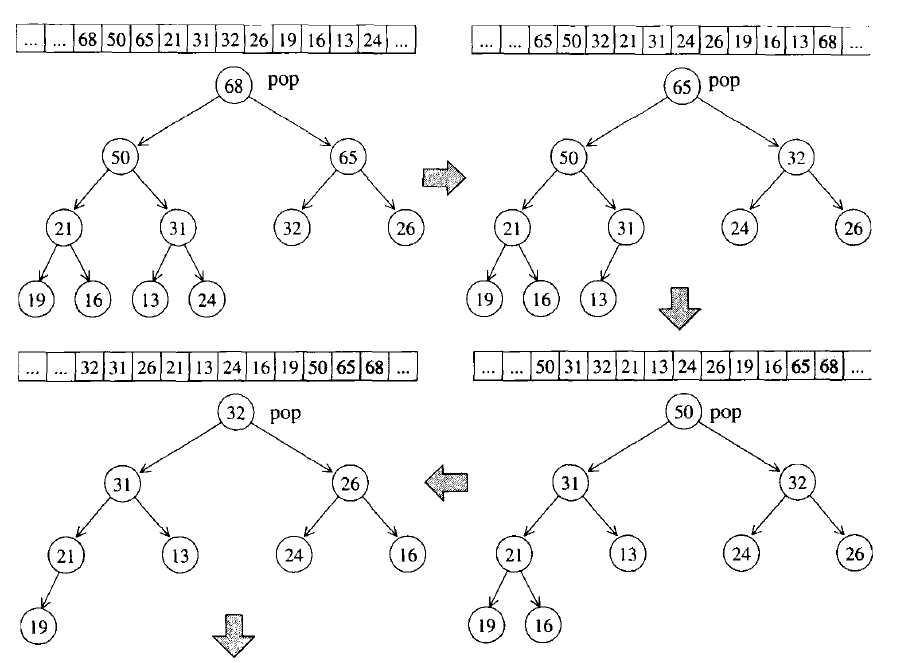
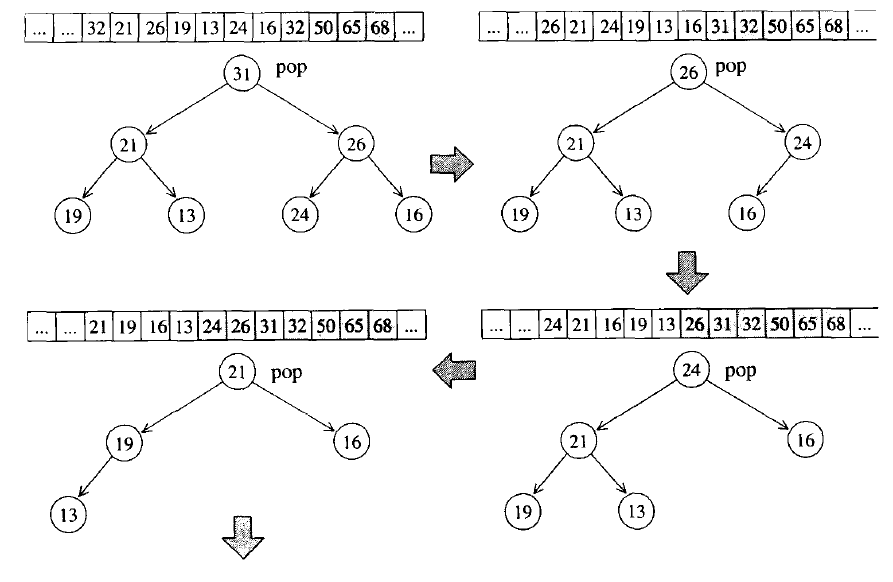
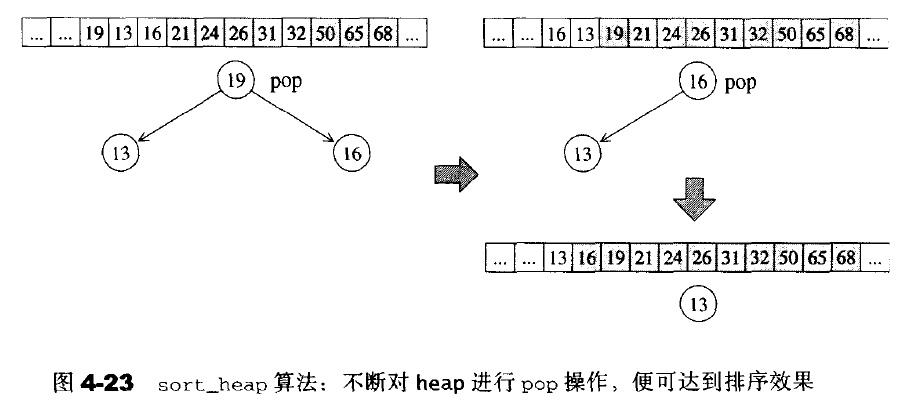
在最大堆的基础上，每次将最大的元素从堆顶弹出(将堆尾部的元素和堆顶元素交换)，然后重新调整堆保持最大元素在堆顶。来看一下整个下溯过程的示意图：

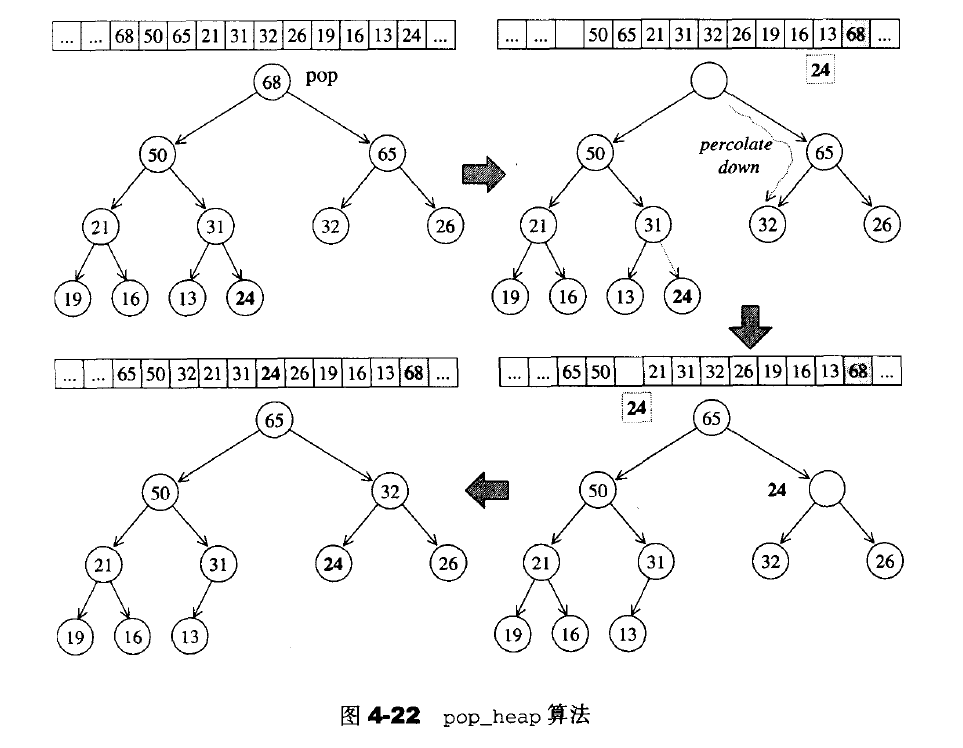
// 调用此函数时，原本数组在最后的元素替换到了现在的堆顶，堆长度也减少了1
void adjust_heap(int* arr, int length){
    int holeIndex = 0;
    int rightChild = 2 * holeIndex + 2;
    int leftChild;
    while(rightChild <= length - 1)
    {
        leftChild = rightChild - 1;
        if (arr[leftChild] > arr[rightChild]){
            swap(arr[leftChild], arr[holeIndex]);
            holeIndex = leftChild;
        }
        else{
            swap(arr[rightChild], arr[holeIndex]);
            holeIndex = rightChild;
        }
        rightChild = 2 * holeIndex + 2;
    }

    // 如果存在左子节点，但不存在右子节点了
    leftChild = rightChild - 1;
    if (leftChild <= length - 1){
        if (arr[leftChild] > arr[holeIndex])
            swap(arr[leftChild], arr[holeIndex]);
    }
    return;
}

这里可以看到，每次调整堆保持为最大堆时，需要下溯把堆顶元素一次次和它的左右字节点比较,直到都大于其左右子节点。下次调整堆又从堆顶下溯，如果内存缓存页表不多时，就需要频繁调度缺失的页。

堆排序

void HeapSort(int* arr, int length){
    if (arr == nullptr || length <1) return;
    make_heap(arr, length);
    for(int i = length - 1, n = length; i > 0; --i, --n){
        swap(arr[i], arr[0]);
        adjust_heap(arr, n);
    }
}

至此，完整的堆排序结束了。最后看一下排序过程示意图：